Randbedingungen an gekrümmten Grenzflächen zwischen einem porösen Medium und einem freien Fluid
| Arbeitsgruppe: | Ehemalige AG Modellierung und PDEs |
| Leitung: | Prof. Dr. Michael Böhm (E-Mail: mbohm@math.uni-bremen.de ) |
| Bearbeitung: | Dr. Sören Dobberschütz |
| Projektpartner: | |
| Laufzeit: | seit 01.08.2008 |
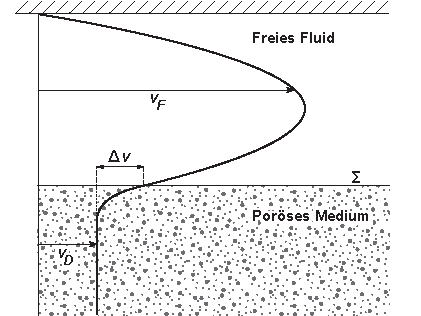
Das Problem, welcher Randbedingung eine viskose Flüssigkeit an der Oberfläche eines porösen Mediums genügt, ist (weiterhin) eine aktuelle Fragestellung. Sinken etwa Marineaggregate auf den Meeresboden (vgl. a. das Projekt „Modellierung und Analysis periodischer Medien mit niederdimensionalen Strukturen“), fließt ein Teil des Wassers an den porösen Partikeln vorbei, während ein anderer Teil durch das Aggregat hindurchfließt. Die jeweiligen Anteile werden stark von dem Verhalten des Wassers direkt an der Grenze beider Medien bestimmt. Um eine möglichst genaue Vorhersage, etwa über aus dem Marineaggregat ausgewaschene Mineralien zu erhalten, ist somit eine genaue Kenntnis dieser Randbedingung nötig.
Seit den 70er Jahren des vorangegangenen Jahrhunderts gibt es sowohl experimentelle als auch theoretische Erkenntnisse zu dieser Fragestellung. Dabei ergibt sich die sogenannte Randbedingung von Beavers und Joseph, deren wichtigstes Merkmal ein Sprung der Geschwindigkeit in tangentialer Richtung ist. Allerdings weisen alle bisherigen Ergebnisse einen entscheidenden Nachteil auf: Diese beziehen sich nur auf ebene Grenzflächen; der Fall einer gekrümmten Berandung ist sowohl experimentell als auch theoretisch bislang nicht behandelt worden – obwohl gerade dieser Fall in der Praxis der relevantere ist. In diesem Projekt wird daher versucht, theoretische Erkenntnisse für allgemeinere Randgeometrien zu erzielen.
Bislang wurde der Fall eines 2-dimensionalen Gebiets mit periodischer Grenzfläche betrachtet. Es zeigt sich, dass die Geometrie des Randes einen Einfluss auf die Randbedingung hat; für die Stärke des o.g. Sprungs ergibt sich ein neuer additiver Anteil aufgrund der gekrümmten Grenzfläche. Da bisher noch nichts über die Größenordnung dieser neuen Effekte bekannt ist, wird sich die weitere Forschung mit der Simulation und Berechnung der Sprunggrößen beschäftigen.

