Ein B.-Step Korrekturverfahren zur numerischen Lösung nichtlineare Optmierungsprobleme
| Arbeitsgruppe: | AG Optimierung und Optimale Steuerung |
| Leitung: | Prof. Dr. Christof Büskens ((0421) 218-63861, E-Mail: bueskens@math.uni-bremen.de ) |
| Bearbeitung: | Dr. Tim Nikolayzik |
| Projektpartner: | |
| Laufzeit: | seit 01.10.2007 |
 Numerische Lösungsverfahren für nichtlineare Optmierungsprobleme benutzten in der Vergangenheit Updatetechniken nach Broyden-Fletcher-Goldfarb-Shanno (BFGS) um Näherungen der Hessematrix der Lagrange-Funktion durchzuführen. Diese Updatetechniken hatten den Vorteil, dass die Approximation der Hessematrix automatisch positiv definit ist und dadurch darauf aufbauende weiterführende Rechnungen leichter durchzuführen sind. Ein weiterer Vorteil liegt in der schnellen Berechenbarkeit bei kleinen und mittelgroßen Optimierungsproblemen. Ein großer Nachteil ist allerdings, dass die so erhaltenen Hessematrixapproximationen dichtbesetzt sind. Dies führt dazu, dass hochdimensionale, schwachbesetzte nichtlineare Optimierungsprobleme nicht mehr effizient gelöst werden können. Aus diesem Grund wird im nichtlinearen Optimierungsproblemlöser WORHP, der speziell auf hochdimensionale, schwachbesetzte Probleme zugeschnitten ist, in jedem Iterationsschritt die exakte Hessematrix sowie die exakten Gradienten zur Verfügung gestellt. Durch diese Vorgehensweise ist es einerseits möglich mit WORHP diese Problem zu lösen und andererseits weitere Verbesserungsstrategien, zur Beschleunigung der Konvergenz, durchzuführen.
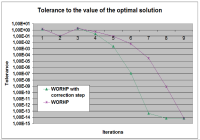
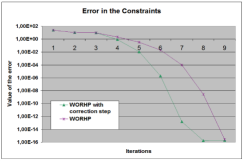
Numerische Lösungsverfahren für nichtlineare Optmierungsprobleme benutzten in der Vergangenheit Updatetechniken nach Broyden-Fletcher-Goldfarb-Shanno (BFGS) um Näherungen der Hessematrix der Lagrange-Funktion durchzuführen. Diese Updatetechniken hatten den Vorteil, dass die Approximation der Hessematrix automatisch positiv definit ist und dadurch darauf aufbauende weiterführende Rechnungen leichter durchzuführen sind. Ein weiterer Vorteil liegt in der schnellen Berechenbarkeit bei kleinen und mittelgroßen Optimierungsproblemen. Ein großer Nachteil ist allerdings, dass die so erhaltenen Hessematrixapproximationen dichtbesetzt sind. Dies führt dazu, dass hochdimensionale, schwachbesetzte nichtlineare Optimierungsprobleme nicht mehr effizient gelöst werden können. Aus diesem Grund wird im nichtlinearen Optimierungsproblemlöser WORHP, der speziell auf hochdimensionale, schwachbesetzte Probleme zugeschnitten ist, in jedem Iterationsschritt die exakte Hessematrix sowie die exakten Gradienten zur Verfügung gestellt. Durch diese Vorgehensweise ist es einerseits möglich mit WORHP diese Problem zu lösen und andererseits weitere Verbesserungsstrategien, zur Beschleunigung der Konvergenz, durchzuführen.Mit Hilfe der parametrischen Sensitivitätsanalyse ist es möglich eine Beschleunigung von NLP-Solvern zu erreichen. SQP-Verfahren, wie WORHP, lösen in jeder Iteration quadratische Teilprobleme. Diese Teilprobleme benutzen linearisierte Nebenbedingungen, so dass die Lösungen dieser Teilprobleme jedoch im Allgemeinen nicht nichtlineare Nebenbedingungen exakt erfüllen. Dieser Fehler ist sehr leicht und ohne großen Aufwand messbar, da nur eine zusätzliche Auswertung der Nebenbedingungen nötig ist. Da WORHP die exakte Hessematrix zur Verfügung stellt und im quadratischen Teilproblem die KKT-Matrix schon zerlegt wurde, ist es damit möglich die Sensitivitätsdifferentiale fast ohne zusätzlichen Rechenaufwand zu bestimmen. Der Korrekturschritt ergibt sich als Produkt der Sensitivitätsdifferentialen und den Vektor der Nebenbedingungen. Die am Lehrstuhl entwickelte Theorie sagt für die korrigierte Iterierte eine Verbesserung in den Nebenbedingungen sowie in der Zielfunktion voraus, die durch erste numerische Tests bestätigt wurden. Die so vorgenommene effiziente Korrektur wird B-Step genannt.