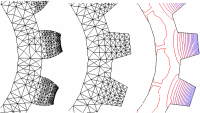
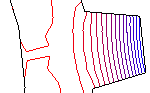Bei der Modellierung von vielen physikalischen Problemen treten gekoppelte Systme auf, deren Komponenten stark unterschiedliches Verhalten (Glattheit der Lösungen etc.) im betrachteten Gebiet zeigen. Eine optimale Diskretisierung zur numerischen Simulation solcher Systeme sollte diesem Verhalten angepasst sein und somit lokal unterschiedlich verfeinerte Rechengitter für unterschiedliche Komponenten verwenden.

Das Forschungsprojekt behandelt adaptive Finite-Elemente-Methoden für stationäre und zeitabhängige gekoppelte Probleme. Zur Diskretisierung der Variablen werden Finite-Elemente-Räume verwendet, die auf unterschiedlich lokal verfeinerten, simplizialen Gittern, ausgehend von der gleichen Makro-Triangulierung des Gebiets, beruhen. Die unterschiedlich verfeinerten Gitter beinhalten dadurch eine hierarchische Struktur, die eine effiziente Implementierung der Kopplungsterme in den Gleichungen ermöglichen. Die adaptive Steuerung der einzelnen Gitter geschieht durch problemangepasste a posteriori Fehlerindikatoren, die getrennte Verfeinerungskriterien für die unterschiedlichen Komponenten bestimmen. Die Methoden werden bereits auf die folgenden gekoppelten Probleme angewandt:

• Thermo-Elastizität mit fest-fest Phasenübergängen.
• Modellierung von thermisch gesteuerten Phasenübergängen durch Phasenrelaxation und Phasenfeldprobleme.
• Wärmeleitung in Flüssigkeiten mit thermischer Konvektion.
• Flüssig-fest Phasenübergänge mit Konvektion in der Schmelze.

Die Finite-Elemente-Implementierung und Anwendungen basieren auf der gemeinsam mit Kunibert Siebert (Augsburg, vormals Freiburg) entwickelten Finite-Elemente-Toolbox ALBERT. Die angepassten Fehlerschätzer zu Phasenübergangsproblemen basieren auf den gemeinsamen Arbeiten mit Z. Chen (Beijing, China), R. Nochetto (College Park, USA) und C. Verdi (Mailand, Italien), siehe Projekt Fehlerabschätzungen und adaptive Finite-Elemente-Methoden für Phasenübergangsprobleme.