Effiziente Verfahren für die Emissionstomographie
| Arbeitsgruppe: | AG Technomathematik |
| Leitung: | Prof. Dr. Dr. h.c. Peter Maaß ((0421) 218-63801, E-Mail: pmaass@math.uni-bremen.de ) |
| Bearbeitung: | Dr. Volker Dicken |
| Projektförderung: | DAAD |
| Projektpartner: | Prof. Dr. Zou, The Chinese University of Hongkong |
| Laufzeit: | 01.01.1999 - 31.12.2001 |

Methoden der Computer-Tomographie werden bei zahlreichen Anwendungen in der diagnostischen Medizin und der zerstörungsfreien Materialprüfung erfolgreich eingesetzt. Beim Einsatz von speziellen SPECT-Tomographen (single photon emission computerized tomography) wird ein radioaktiv markiertes Präparat injiziert, die Strahlung Rmuf dieses Präparats wird außerhalb des Körpers gemessen. Bei dieser Anwendung muss sowohl die Gewebedichte mu des untersuchten Objekts als auch die Verteilung des radioaktiven Präparates f bestimmt werden:
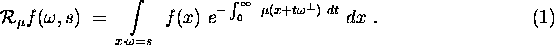
Klassische Rekonstruktionsverfahren berücksichtigen den Einfluss der Dichtefunktion mu nur grob oder benötigen aufwendige Zusatzmessungen zu ihrer Bestimmung. Neue mathematische Techniken aus dem Gebiet der nichtlinearen inversen Probleme ermöglichen es, mu zusammen mit f aus den SPECT-Daten allein zu bestimmen.
In diesem Projekt hat die AG Technomathematik Tikhonov-Regularisierungen zur Inversion der gedämpften Radon-Transformation (1) untersucht. Eine Approximation der Lösung wurde dabei durch Minimierung des Funktionals
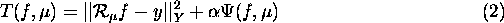
gefunden. Auf der theoretischen Seite des Projekts wurden die Konvergenzeigenschaften dieser Regularisierung und verallgemeinerte Strafterme Psi untersucht. Andererseits wurden effiziente numerische Verfahren zur Minimierung des nichtlinearen Tikhonov-Funktionals (2) entwickelt, implementiert und getestet. Dazu wurden Gauß-Newton-Verfahren eingesetzt und die resultierenden linearen Gleichungssysteme mit CG-Verfahren gelöst.
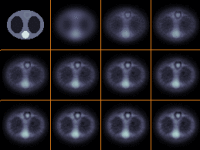
In Kooperation mit Prof. Zou (Hongkong) werden weiterführende Untersuchungen mit differenzierbaren BV-Straftermen durchgeführt. Damit können bei zahlreichen linearen Problemen sehr gute Ergebnisse erzielt werden, die Minimierung solcher nichtquadratischen Strafterme hat jedoch einen noch größeren numerischen Aufwand zur Folge.


