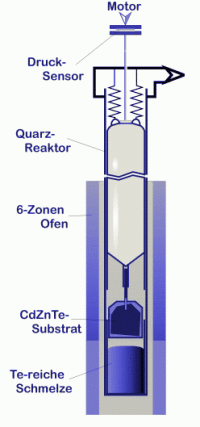
Simulation und Optimierung der Flüssigphasenepitaxie bei der Herstellung von Infrarotdetektoren
| Arbeitsgruppe: | AG Numerik PDE |
| Leitung: | Prof. Dr. Alfred Schmidt ((0421) 218-63851, E-Mail: alfred.schmidt@uni-bremen.de ) |
| Bearbeitung: | |
| Projektförderung: | BMBF (Universität Freiburg) |
| Projektpartner: |
Institut für Angewandte Mathematik, Universität Freiburg Kristallographisches Institut, Universität Freiburg AEG Infrarot-Module GmbH, Heilbronn |
| Laufzeit: | 01.10.2000 - 31.12.2003 |

Bei der Herstellung von Infrarotdetektoren ist das Aufwachsen der aktiven Detektorschicht der bestimmende Faktor für die Güte der erhaltenen Detektoren. Die entscheidenden Faktoren für das Kristallwachstum sind die Temperatur- und Konzentrationsverteilung von Quecksilber, Cadmium und Tellur in der flüssigen Phase. Die mathematische Modellierung führt auf ein System aus den inkompressiblen Navier-Stokes-Gleichungen in Boussinesq-Approximation für Geschwindigkeit und Druck, sowie der Energiebilanz für die Temperatur und der Massebilanz für die Konzentrationen. Die Wachstumsgeschwindigkeit der Epitaxieschicht ergibt sich dabei aus den Stefan-Bedingungen für die Temperatur und den Konzentrationen der einzelnen Komponenten. Durch numerische Simulationen der Temperaturverteilung im gesamten Ofen sowie dieses Systems innerhalb des Epitaxietiegels in zwei und drei Raumdimensionen sollen Züchtungsbedingungen bestimmt werden, die ein homogenes Wachstum der Detektorschicht ermöglichen.
Für die Simulation im Epitaxietiegel müssen neue mathematische
Verfahren hergeleitet werden, die eine genaue Bestimmung von W
achstumsrate und Dicke der Detektorschicht erlauben.
Dieses schließt die Entwicklung von adäquaten Fehlerschätzern
bzw. -indikatoren für diese Größen sowie selbstadaptiven Methoden
zur Simulation des Aufwachsens mit ein.
Das Projekt steht unter der Leitung von Prof. Dziuk
(Institut für Angewandte Mathematik, Freiburg) und
wird im Rahmen des BMBF-Programms "Neue mathematische
Verfahren in Industrie und Dienstleistung" gefördert.
Nähere Informationen unter http://www.mathematik.uni-freiburg.de/IAM/Research/projectsdz/epitaxie/