DFG-SPP 1114: Optimal Control of Degenerate Parabolic Partial Differential Equations in Medical Image Processing
| Working Group: | WG Industrial Mathematics |
| Leadership: | Prof. Dr. Dr. h.c. Peter Maaß ((0421) 218-63801, E-Mail: pmaass@math.uni-bremen.de ) |
| Processor: | Prof. Dr. Kristian Bredies |
| Funding: | DFG SPP 1114 |
| Project partner: | Centrum für komplexe Systeme und Visualisierung (CeVis), Bremen |
| Time period: | 01.01.2005 - 30.09.2007 |
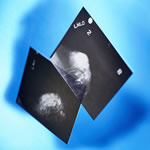
The mathematical objective of this project consists in controlling degenerate diffusion equations to an optimal degree, the control having an effect on the diffusion coefficients. These types of problem occur in medical image processing, for example when optimising the presentation of mammography data.
The analysis of mammography data by medical experts can be modelled as a process on various scales. The doctor analyses the image at various levels of resolution in order to obtain both a detailed impression of small details as well as a complete overview of the position of critical patterns. This multiscale process will be graphically supported by the presentation of a succession of images instead of a single image. This succession of images emphasises the different phases of the investigation by making different image details stand out at different scalings. This film is produced by solving an optimal control problem for a parabolic diffusion equation.
The control of diffusion equations via the diffusion coefficients is a demanding mathematical task. In this project, the investigation of these types of optimal control problems ranges from the analysis of the PDEs through the analysis of the algorithms for optimal control and the numerical treatment of the PDEs to the numerical realisation of the algorithms for optimal control. Our objective is to control a degenerate partial differential equation so that the sequence of images which is formed beginning with y0 approaches a similar yk - version for prescribed times 0 < t1 < t2 < . . . < tk = T. One possibility is to minimise the following functional:
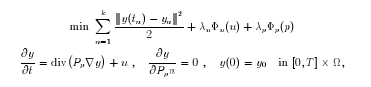
where the diffusion tensor takes the form
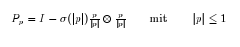
In order to numerically compute the solutions to this control problem, the above parabolic partial differential equation has to be solved repeatedly in each time step. This leads to a demanding task as far as the computing capacity and efficiency of the algorithms and implementation are concerned. In a preparatory project, the optimal control problem for the simpler differential equation
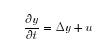
was considered, i.e. the control occurred only via the coefficients.

