DFG-SPP 1114: Optimale Steuerung degenerierter parabolischer partieller Differentialgleichungen in der medizinischen Bildverarbeitung
| Arbeitsgruppe: | AG Technomathematik |
| Leitung: | Prof. Dr. Dr. h.c. Peter Maaß ((0421) 218-63801, E-Mail: pmaass@math.uni-bremen.de ) |
| Bearbeitung: | Prof. Dr. Kristian Bredies |
| Projektförderung: | DFG SPP 1114 |
| Projektpartner: | Centrum für komplexe Systeme und Visualisierung (CeVis), Bremen |
| Laufzeit: | 01.01.2005 - 30.09.2007 |
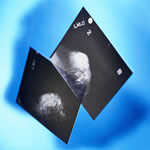
Die mathematische Aufgabe dieses Projekts besteht darin, degenerierte Diffusionsgleichungen optimal zu steuern, wobei die Steuerung auf die Diffusionskoeffzienten wirkt. Solche Art von Problemen treten in der Medizinischen Bildverarbeitung auf, z.B. bei der Optimierung der Präsentation von Mammographie-Daten.
Die Untersuchung von Mammographie-Daten durch medizinische Experten kann als Prozess auf unterschiedlichen Skalen modelliert werden. Der Arzt wertet das Bild auf unterschiedlichen Auflösungsstufen aus, um sowohl einen detaillierten Eindruck kleiner Details wie auch einen Gesamtüberblick von der Lage kritischer Muster zu gewinnen. Dieser Multiskalenprozess soll durch die Präsentation einer Bildfolge anstelle eines einzigen Bildes graphisch unterstützt werden. Diese Bildfolge betont die unterschiedlichen Untersuchungsphasen, indem verschiedene Bilddetails zu unterschiedlicher Skalierung hervorgehoben werden. Dieser Film wird dadurch erzeugt, dass man ein optimales Steuerungsproblem für eine parabolische Diffusionsgleichung löst.
Die Steuerung von Diffusionsgleichungen uber den Diffusionskoeffzienten ist eine anspruchsvolle mathematische Aufgabe. Die Untersuchung dieser Art von Optimal-Steuerungs-Probleme in diesem Projekt reicht von der Analyse der PDEs, uber die Analyse der Algorithmen für die optimale Steuerung und der numerischen Behandlung der PDEs, bis zur numerischen Realisierung der Algorithmen zur optimalen Steuerung.
Unser Ziel ist es, eine degenerierte partielle Differentialgleichung zu steuern, so dass die entstehende Bildsequenz beginnend mit y0 sich einer ähnlichen yk - Version annähert, für festgelegte Zeitpunkte 0 < t1 < t2 < . . . < tk = T. Eine Möglichkeit besteht darin, das folgende Funktional zu minimieren:
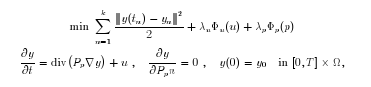
wobei der Diffusionstensor die Form
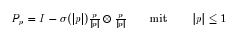
hat.
Um die Lösungen dieses Steuerungsproblems numerisch zu berechnen, ist es nötig, die oben genannte parabolische partielle Differentialgleichung mehrfach in jedem Zeitschritt zu lösen. Dies führt zu einer anspruchsvollen Aufgabe in Bezug auf Rechenleistung und Effzienz der Algorithmen und Implementierung. In einem vorbereitenden Projekt wurde das Optimalsteuerungsproblem für die einfachere Differentialgleichung
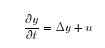
betrachtet, d.h. die Steuerung fand nur über die Koeffzienten statt.

