Der gemeinsame Spektralradius von Matrizenmengen
| Leitung: | Prof. Dr. Fabian Wirth |
| Bearbeitung: | |
| Projektpartner: |
Prof. Dr. Vincent Blondel, Université catholique de Louvain, Belgien Jacques Theys, Université catholique de Louvain, Belgien Dr. Nicola Guglielmi, Università di L'Aquila, Italien Prof. Dr. Marino Zennaro, Università di Trieste, Italien |
| Laufzeit: | seit 01.07.2002 |
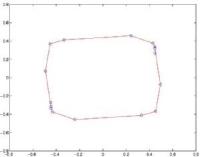
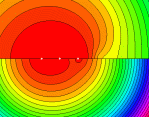 Der gemeinsame Spektralradius einer Matrizenmenge beschreibt das maximale exponentielle Wachstum, das beliebige Produkte von Matrizen aus dieser Menge erreichen können. Diese Größe bestimmt interessante Eigenschaften in vielen Zusammenhängen, die durch eine Menge von Matrizen beschreibbar sind. So charakterisiert sie etwa exponentielle Stabilität bestimmter zeitvarianter, linearer Systeme, ist entscheidend bei der Untersuchung des Konvergenzverhaltens von Markov-Ketten, bei Regularitätsuntersuchungen von Wavelets, bei Kapazitätsberechnungen in der Kodierungstheorie und in der Bestimmung von Eigenschaften von Grenzobjekten iterierter Funktionensysteme. Es ist bekannt, dass die Berechnung des gemeinsamen Spektralradius einer endlichen Matrizenmenge ein NP-schweres Problem ist. Aufgrund seiner Wichtigkeit sind dennoch effiziente Algorithmen (im Rahmen des Möglichen) von großem Interesse. Eine wünschenswerte Eigenschaft von Matrizenmengen, die interessante Verfahren zur Berechnung erlaubt, ist die so genannte Endlichkeitsbedingung, von der allerdings vor kurzem gezeigt wurde, dass sie nicht immer erfüllt ist. Diese Bedingung besagt, dass der gemeinsame Spektralradius stets durch den Spektralradius eines endlichen Produkts angenommen wird. In diesem Forschungsprojekt werden Methoden untersucht, die Grundlagen einer Berechnung des gemeinsamen Spektralradius bilden können. So wurde für eine Klasse von Spezialfällen gezeigt, dass sie die Endlichkeitsbedingung erfüllen, und es wurden Methoden zur expliziten Konstruktion extremaler Normen entwickelt. Auf Grundlage dieser Resultate sollen nun neue Verfahren zur Berechnung des gemeinsamen Spektralradius entwickelt werden. Wir vermuten, dass die Endlichkeitsbedingung generisch erfüllt ist, und arbeiten an einer Beweisidee für diese Vermutung. Weitere Untersuchungen beschäftigen sich mit der Frage, welche Eigenschaften Matrizenfolgen erfüllen, deren Produkte den gemeinsamen Spektralradius approximieren. Insbesondere wird dabei analysiert, wie oft jede einzelne Matrix im langen Mittel in optimalen Produkten auftaucht, und wann dieses optimale Verhältnis in einer Sturmschen Folge realisiert wird.
Der gemeinsame Spektralradius einer Matrizenmenge beschreibt das maximale exponentielle Wachstum, das beliebige Produkte von Matrizen aus dieser Menge erreichen können. Diese Größe bestimmt interessante Eigenschaften in vielen Zusammenhängen, die durch eine Menge von Matrizen beschreibbar sind. So charakterisiert sie etwa exponentielle Stabilität bestimmter zeitvarianter, linearer Systeme, ist entscheidend bei der Untersuchung des Konvergenzverhaltens von Markov-Ketten, bei Regularitätsuntersuchungen von Wavelets, bei Kapazitätsberechnungen in der Kodierungstheorie und in der Bestimmung von Eigenschaften von Grenzobjekten iterierter Funktionensysteme. Es ist bekannt, dass die Berechnung des gemeinsamen Spektralradius einer endlichen Matrizenmenge ein NP-schweres Problem ist. Aufgrund seiner Wichtigkeit sind dennoch effiziente Algorithmen (im Rahmen des Möglichen) von großem Interesse. Eine wünschenswerte Eigenschaft von Matrizenmengen, die interessante Verfahren zur Berechnung erlaubt, ist die so genannte Endlichkeitsbedingung, von der allerdings vor kurzem gezeigt wurde, dass sie nicht immer erfüllt ist. Diese Bedingung besagt, dass der gemeinsame Spektralradius stets durch den Spektralradius eines endlichen Produkts angenommen wird. In diesem Forschungsprojekt werden Methoden untersucht, die Grundlagen einer Berechnung des gemeinsamen Spektralradius bilden können. So wurde für eine Klasse von Spezialfällen gezeigt, dass sie die Endlichkeitsbedingung erfüllen, und es wurden Methoden zur expliziten Konstruktion extremaler Normen entwickelt. Auf Grundlage dieser Resultate sollen nun neue Verfahren zur Berechnung des gemeinsamen Spektralradius entwickelt werden. Wir vermuten, dass die Endlichkeitsbedingung generisch erfüllt ist, und arbeiten an einer Beweisidee für diese Vermutung. Weitere Untersuchungen beschäftigen sich mit der Frage, welche Eigenschaften Matrizenfolgen erfüllen, deren Produkte den gemeinsamen Spektralradius approximieren. Insbesondere wird dabei analysiert, wie oft jede einzelne Matrix im langen Mittel in optimalen Produkten auftaucht, und wann dieses optimale Verhältnis in einer Sturmschen Folge realisiert wird.