DFG-SPP 1114: Mathematische Methoden in der Zeitreihenanalyse und digitalen Bildverarbeitung
| Arbeitsgruppe: | AG Technomathematik |
| Leitung: | Prof. Dr. Dr. h.c. Peter Maaß ((0421) 218-63801, E-Mail: pmaass@math.uni-bremen.de ) |
| Bearbeitung: |
Dr. Stefan Schiffler
Sabine Eifeld (E-Mail: eifeld@math.uni-bremen.de ) |
| Projektförderung: | DFG (Schwerpunktprogramm 1114) |
| Projektpartner: | |
| Laufzeit: | 01.08.2001 - 31.07.2007 |

Das seit August 2001 laufende DFG-Schwerpunktprogramm SPP 1114 "Mathematische Methoden der Zeitreihenanalyse und digitalen Bildverarbeitung", eines von derzeit lediglich sieben mathematischen Schwerpunktprogrammen, ist nach erfolgreicher Evaluation im Sommer 2003 in seine zweite Phase gestartet. In jetzt 21 Teilprojekten forschen Mathematiker, Physiker, Statistiker und andere Wissenschaftler aus verschiedenen deutschen Universitäten zu Fragestellungen der Zeitreihenanalyse und Bildverarbeitung; die Koordination erfolgt nach wie vor vom Zentrum für Technomathematik aus. Der Austausch zwischen Wissenschaftlern, die mit unterschiedlichen Ansätzen und Methoden in den Bereichen Zeitreihenanalyse und digitaler Bildverarbeitung aktiv sind, und der systematische Vergleich von bisher parallel entwickelten Verfahren stehen im Zentrum des SPP 1114.
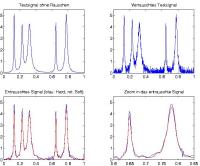
Ein am ZeTeM angesiedeltes Teilprojekt des Schwerpunktprogramms beschäftigt sich gezielt mit dem Vergleich unterschiedlicher Methoden zur Auswertung und Bearbeitung von Zeitreihen bzw. Bilddaten. U.a. wurden in einer mathematisch-theoretischen Untersuchung nichtlineare Wavelet-Methoden analysiert und Analogien zwischen sogenannten Soft- Thresholding-Verfahren und Methoden der Variationsrechnung erforscht. Beim Soft-Thresholding wird ausgenutzt, dass die Koeffizienten eines Signals bezüglich einer Wavelet-Basis bestimmte statistische Eigenschaften haben. Die relevante Information eines Signals verbirgt sich oft in wenigen großen Koeffizienten, während das Rauschen sich in vielen kleinen Koeffizienten niederschlägt. Die Wavelet-Koeffizienten werden also mit einer nichtlinearen Funktion derart verändert, dass das Rauschen weitgehend verschwindet und die relevante Information möglichst erhalten bleibt. Die Methoden aus der Theorie der Funktionenräume hingegen versuchen, ein entrauschtes Signal derart zu finden, dass es sich einerseits nicht viel vom Originalsignal unterscheidet und andererseits eine bestimmte Glattheit (gemessen über die Zugehörigkeit zu bestimmten Funktionenräumen) hat. Das klassische Resultat besagt, dass beide Methoden für bestimmte Funktionenräume die selben Ergebnisse liefern. Dieses Resultat konnte auf andere Thresholding-Methoden, wie zum Beispiel das Hard-Thresholding, erweitert werden. Außerdem konnte gezeigt werden, dass es einen "stetigen" Übergang zwischen dem Soft- und dem Hard-Thresholding gibt.