Numerische Erfassung der Impedanz von Brennstoffzellenmembranen
| Arbeitsgruppe: | AG Technomathematik |
| Leitung: | Prof. Dr. Dr. h.c. Peter Maaß ((0421) 218-63801, E-Mail: pmaass@math.uni-bremen.de ) |
| Bearbeitung: | Dr. Henning Thielemann |
| Projektpartner: | Institut für Keramische Werkstoffe und Bauteile, Universität Bremen |
| Laufzeit: | 01.11.2003 - 31.10.2005 |

Das Institut für Keramische Werkstoffe und Bauteile arbeitet an der Entwicklung von neuartigen Brennstoffzellen mit neuen, hitzebeständigeren Membranen. Um die Leistungsfähigkeit dieser neu entwickelten Membranen zu testen, werden diese an einem Impedanzmessstand geprüft. Das Auswerten durch kommerzielle Anlagen ist kostspielig und zeitaufwendig, außerdem erfährt der Experimentator so nichts über das Auswerteverfahren und kann auch nicht in die Auswertung eingreifen. Deswegen wurde im Institut ein Messstand entwickelt, der diese kommerziellen Auswertungen weitestgehend ersetzen soll. Der neue Messstand ist weniger genau, reicht jedoch aus, um zu testen, ob sich die Leitfähigkeit der Membranen verbessert oder verschlechtert hat.
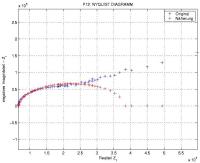
Zur Auswertung werden die Real- und Imaginäranteile der Impedanz in einem Nyquist- Diagramm aufgetragen. Die Messdaten sollten im besten Fall einen Halbkreis darstellen, der für geringe Frequenzen in die Warburg-Gerade übergeht. An ein so angefertigtes Diagramm wurde bisher manuell ein Halbkreis angepasst. Von der Lage und der Größe des Halbkreises lassen sich direkt die charakteristischen Parameter des Modells (zwei Widerstände und eine Kapazität) ablesen. Dies wird nun durch mathematische Methoden automatisiert, so dass direkt nach der Messung die charakteristischen Daten des Modells und ihre Fehler ausgegeben werden können.Die mathematische Aufgabenstellung zerfällt in zwei Teile, die im Rahmen des Modellierungsseminars von den Studierenden Oliver Kermer und Alouane Abdellatif bearbeitet werden: Anpassen eines Halbkreises an Messdaten, die näherungsweise einen Halbkreis beschreiben, sowie die Trennung von Halbkreis und Warburg-Gerade. Für den ersten Teil wurden bislang zwei Ansätze verfolgt: Der aus dem Ersatzschaltbild resultierende Zusammenhang wird auf ein lineares Ausgleichsproblem zurückgeführt. Das umformulierte Optimierungsproblem weist eine recht willkürliche Wichtung der Messwerte auf, die aber durch Kombination mit dem zweiten Ansatz ausgeglichen werden kann. Dabei wird die Frequenz ignoriert, bei der jede einzelne Impedanz gemessen wird, und es erfolgt eine Auswertung (analog zur manuellen Auswertung), die allein durch die Geometrie der Messdaten motiviert ist.
Als problematisch erweist sich, dass die gemessenen Daten von der theoretisch vorhergesagten Halbkreisform abweichen. Anscheinend sind die Daten in einer Richtung gestaucht. Dieses Phänomen konnte bislang zwar nicht physikalisch geklärt werden, immerhin lässt sich aber der Stauchungsfaktor mit zu Halbellipsen erweiterten Modellen bestimmen. Die mit diesen Modellen gefundenen Kurven nähern die Messdaten sehr gut an. Zur Trennung von Halbkreis und Warburg-Gerade werden die oben vorgestellten Verfahren in eine Iteration eingebettet. Hierfür werden verschiedene, auf Gradientenabstiegs- und Newton-Verfahren beruhende Ansätze untersucht.