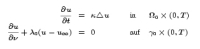Parameteridentifikation bei der Überwachung von Stahlessen
| Working Group: | WG Industrial Mathematics |
| Leadership: | Prof. Dr. Dr. h.c. Peter Maaß ((0421) 218-63801, E-Mail: pmaass@math.uni-bremen.de ) |
| Processor: | |
| Funding: | DAAD und JSPS |
| Project partner: |
Prof. Dr. Masahiro Yamamoto, University of Tokyo, Japan Prof. Dr. Hans-Jürgen Reinhardt, Universität Siegen Prof. Dr. Stephan Dahlke, Universität Marburg |
| Time period: | since 01.01.2003 |

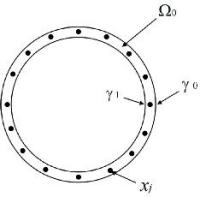
Die Lebensdauer von hohen Schornsteinen an Hochöfen zur Stahlproduktion beträgt nur etwa dreißig Jahre, in dieser Zeit wird das Mauerwerk durch das geschmolzene Eisenerz von innen heraus nach und nach zersetzt. Um eine möglichst lange und sichere Betriebsfähigkeit der Stahlesse zu gewährleisten, muss die Dicke oder äquivalent die Temperatur im Innern des verbliebenen Mauerwerks kontinuierlich überwacht werden. Allerdings kann die Temperatur nur an der Außenseite der Esse sowie an einigen ausgewählten Punkten im äußersten Teil des Mauerwerks gemessen werden.
Mathematisch kann dies durch eine Wärmeleitungsgleichung auf einem kreisförmigen Zylinder (Geometrie der Stahlesse) modelliert werden, dabei sind die Randwerte am inneren Rand der Stahlesse unbekannt. Dies führt auf ein Problem der Parameteridentifikation für die Wärmeleitungsgleichung – ein nichtlineares, inverses Problem: In dieser deutsch-japanischen Kooperation, die vom DAAD und der Japan Society for the Promotion of Science (JSPS) unterstützt wird, werden sowohl Stabilitätsuntersuchungen für das inverse Problem durchgeführt als auch numerische Verfahren zur Rekonstruktion der Randdaten und damit zur Bestimmung der Wärmeverteilung im Innern des Mauerwerks entwickelt. Hierbei sollen die Ergebnisse adaptiver Wavelet-Verfahren mit den Rekonstruktionen aus Finite-Elemente-Simulationen verglichen werden. Erste Ergebnisse wurden bereits in der Diplomarbeit von Christian Fröbel zusammengefasst.