Micro–macro modelling of reaction–diffusion processes in multi-phase materials
| Working Group: | Former WG Modelling and PDEs |
| Leadership: | Prof. Dr. Michael Böhm (E-Mail: mbohm@math.uni-bremen.de ) |
| Processor: |
Dr. Sören Dobberschütz
Prof. Dr. Malte Peter Dr. Sebastian Meier Prof. Dr. Hari Shankar Mahato |
| Funding: | SCiE, Studienstiftung, Zentrale Forschungsförderung Universität Bremen |
| Project partner: | |
| Time period: | since 01.03.2004 |
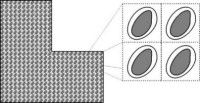
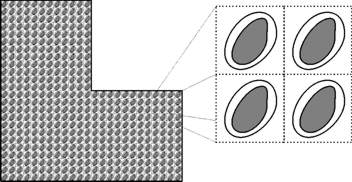 Nowadays, many materials used in industry consist of several phases, i.e. they consist of two or more finely interwoven materials (with different physical and chemical properties). Typical examples are glass- and carbon-reinforced plastics as well as porous materials such as concrete. In order to describe the observable (macroscopic) properties of such composites, it is necessary to include information about the microscopic structure, i.e. knowledge about the interweavement or the pore structure in case of a porous material, as well as the properties of each component. For this purpose, general coupled systems of parabolic partial differential equations are considered, which, in particular, describe reaction–diffusion processes in multi-phase materials.
Nowadays, many materials used in industry consist of several phases, i.e. they consist of two or more finely interwoven materials (with different physical and chemical properties). Typical examples are glass- and carbon-reinforced plastics as well as porous materials such as concrete. In order to describe the observable (macroscopic) properties of such composites, it is necessary to include information about the microscopic structure, i.e. knowledge about the interweavement or the pore structure in case of a porous material, as well as the properties of each component. For this purpose, general coupled systems of parabolic partial differential equations are considered, which, in particular, describe reaction–diffusion processes in multi-phase materials.
Field 1: Mathematical homogenisation
Using mathematical averaging techniques (homogenisation), it is possible to obtain macro-models from the micro-models, which reflect the observable processes and which can be solved with considerably less numerical effort than the corresponding micro-models. For this purpose, the geometry of the sample is assumed periodic with respect to a scale parameter ε (a typical pore diamter, e.g.), also cf. fig. 1. This leads to microscopic systems of equations with periodic coefficients. The corresponding macroscopic problem is obtained by passing to the limit as ε -> 0.Depending on the relevance of the different processes taking place on the microscopic scale, different types of macro-models are obtained from (structurally) the same micro-models. Specifically, the non-dimensionalisation yields systems of equations with different scalings of the material parameters (diffusivites, conductivities, ...) with powers of the scale parameter ε. This results in structurally different types of macro-models when passing to the limit. One objective is to find the critical values and ranges of the powers for which the same types of macro-models result. From a physical point of view, this question can be reformulated as follows: How (or in which form) is the influence of certain processes taking place on the microscopic scale reflected in the macro-model? This concept is intended to allow in advance the determination which type of macro-model is suitable for a certain problem.
Moreover, it is well-known that chemical corrosion processes in multi-phase materials often induce a change in the micro-structure of the material. It is investigated how this temporally and spatially local change of the micro-structure can be accounted for in the homogenisation procedure.
Field 2: Two-scale models
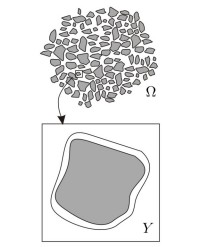
For a characteristic choice of scaling parameters, the mathematical homogenisation leads to the so-called two-scale models. In such a model, a reference cell is considered in each macroscopic point of the material, in which the processes are modelled which are relevant at the pore scale (fig. 2). They influence the macroscopic quantities via coupling terms. Such models are already successfully applied to simulate flow in fissured media as well as to determine effective material behaviour in solid mechanics. Although requiring an increased numerical effort, processes at the pore scale can be resolved much better by two scale models compared to pure macroscopic models. While the mathematical homogenization admits a classification of the range of parameters and the geometries for which two-scale models are appropriate and to determine the parameters in these models, it is also possible to propose a two-scale model independent of the homogenization context. By this means, one can consider more general, nonlinear models. In particular, the periodicity condition on the medium can be dropped. The mathematical investigation of these models and their solutions is the basic goal in this field.The modelling of a temporally evolving micro-structure is also of special interest in this field. For example, in unsaturated porous media, the pore-water distribution can highly influence the contaminant transport in the pore space. We are looking for models that can properly describe such effects.
As a practical application, we currently investigate prediction models for concrete carbonation (also see the project Moving-boundary models for concrete carbonation).