Mikro-Makro-Modellierung von Reaktions-Diffusions-Prozessen in Mehrphasen-Materialien
| Arbeitsgruppe: | Ehemalige AG Modellierung und PDEs |
| Leitung: | Prof. Dr. Michael Böhm (E-Mail: mbohm@math.uni-bremen.de ) |
| Bearbeitung: |
Dr. Sören Dobberschütz
Prof. Dr. Malte Peter Dr. Sebastian Meier Prof. Dr. Hari Shankar Mahato |
| Projektförderung: | SCiE, Studienstiftung, Zentrale Forschungsförderung Universität Bremen |
| Projektpartner: | |
| Laufzeit: | seit 01.03.2004 |
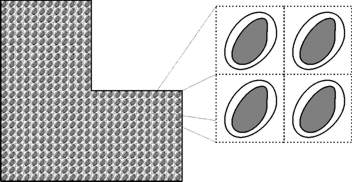 Viele der heute industriell verwendeten Materialien bestehen aus mehreren Phasen, d.h. sie bestehen aus zwei oder mehreren, fein verflochtenen Materialien mit verschiedenen physikalischen oder chemischen Eigenschaften. Typische Beispiele sind Glas- oder Kohlefaser-verstärkte Kunststoffe sowie poröse Materialien wie Beton. Um die beobachtbaren (Makro-) Eigenschaften solcher Komposite zu beschreiben, ist es notwendig, Informationen über die Mikro-Struktur einzubeziehen, d.h. das Wissen über die Verflechtungen bzw. die Porenstruktur bei porösen Materialien, sowie die Eigenschaften der einzelnen Bestandteile zu nutzen.
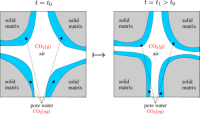
Viele der heute industriell verwendeten Materialien bestehen aus mehreren Phasen, d.h. sie bestehen aus zwei oder mehreren, fein verflochtenen Materialien mit verschiedenen physikalischen oder chemischen Eigenschaften. Typische Beispiele sind Glas- oder Kohlefaser-verstärkte Kunststoffe sowie poröse Materialien wie Beton. Um die beobachtbaren (Makro-) Eigenschaften solcher Komposite zu beschreiben, ist es notwendig, Informationen über die Mikro-Struktur einzubeziehen, d.h. das Wissen über die Verflechtungen bzw. die Porenstruktur bei porösen Materialien, sowie die Eigenschaften der einzelnen Bestandteile zu nutzen. Mithilfe mathematischer Mittelungsmethoden wie der periodischen Homogenisierung ist es möglich, aus den Mikro-Modellen Makro-Modelle zu gewinnen, welche die beobachtbaren Prozesse widerspiegeln, und die sich im Gegensatz zu den Mikro-Modellen mit wesentlich geringerem Aufwand numerisch lösen lassen. Von besonderem Interesse bei diesem Projekt sind Mikrostrukturen, die durch den Prozess verändert werden. Diese Situation ist z.B. bei der Karbonatisierung von Beton wichtig, dadurch dass die Porenkanäle durch Anlagerung von Reaktionsprodukten verengt werden. In der 2006 fertiggestellten Dissertation von Malte Peter wurde gezeigt, dass eine zeitlich und örtlich lokale Veränderung der Mikrostruktur bei der Homogenisierung berücksichtigt werden kann. Die Idee basiert auf einer Koordinatentransformation auf eine periodische Geometrie. Aus dieser Arbeit resultierten 2007 und 2008 mehrere Publikationen.
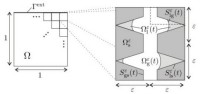
Die mathematische Homogenisierung führt in bestimmten Fällen auf sogenannte Zwei-Skalen-Modelle. Dabei wird in jedem makroskopischen Punkt des Mediums eine Referenzzelle angenommen, in der die auf Porenebene relevanten Prozesse modelliert werden. Gegenüber reinen Makro-Modellen können dabei Prozesse auf der Porenebene wesentlich besser aufgelöst werden.
Auch hier liegt eine wesentliche Schwierigkeit bei der Modellierung der sich zeitlich ändernden Mikrostruktur. In ungesättigten porösen Medien kann insbesondere die Verteilung des Porenwassers den Transport von Substanzen im Porenraum stark beeinflussen. In der 2008 fertiggestellten Dissertation von Sebastian Meier wurden auf Basis der Homogenisierung Modelle entwickelt, die solche Effekte mit einbeziehen können. Die mathematische Theorie zu diesen Modellen ist auf Grund von Nichtlinearitäten und Degenerierung der Gleichungen sehr komplex und stellt den Schwerpunkt der Arbeit dar. Die Anwendung der Zwei-Skalen-Modelle auf die Karbonatisierung von Beton wurde in einer weiteren Forschungsarbeit weiterentwickelt.
Aktuell werden Diffusions-Reaktionsgleichungen mit hoch-nichtlinearen Reaktionsraten in nicht-Hilbertraum-Settings sowie zeitlich veränderliche niederdimensionale Strukturen untersucht (vgl. a. das Projekt „Modellierung und Analysis periodischer Medien mit niederdimensionalen Strukturen“).