Streuung von Wasserwellen an Reihen identischer Körper
| Leitung: | Prof. Dr. Malte Peter |
| Bearbeitung: | |
| Projektpartner: |
M. H. Meylan, University of Auckland, Neuseeland C. M. Linton, Loughborough University, Großbritannien |
| Laufzeit: | seit 01.03.2004 |
 Die Streuung und Beugung von Wasserwellen an sich im Wasser befindenden oder an der Oberfläche schwimmenden Körper ist von großer praktischer Bedeutung in verschiedenen Anwendungsfeldern, z.B. bei der Konstruktion von Strukturen auf dem Meer (Ölbohrplattformen, Windkraftanlagen usw.) und in der Klimaforschung (Streuung an Feldern von Eisschollen).
Die Streuung und Beugung von Wasserwellen an sich im Wasser befindenden oder an der Oberfläche schwimmenden Körper ist von großer praktischer Bedeutung in verschiedenen Anwendungsfeldern, z.B. bei der Konstruktion von Strukturen auf dem Meer (Ölbohrplattformen, Windkraftanlagen usw.) und in der Klimaforschung (Streuung an Feldern von Eisschollen).
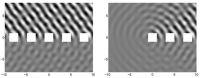
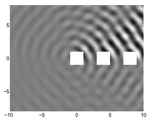
Viele technische Strukturen (Antennen, Offshore-Platformen usw.) bestehen aus sich wiederholenden Elementen mit gleichen Abständen. In vielen praktischen Anwendungen ist es sinnvoll, das komplexe Mehr-Körper-Streuungsproblem durch eines zu ersetzen, in dem die Elemente in einer unendlichen Reihe angeordnet sind, d.h. die Körper sind entlang einer Geraden angeordnet. Falls die einlaufenden Wellen auch periodisch sind, ist das resultierende Streuungsproblem aufgrund der Periodizität wesentlich einfacher. In diesem Fall kann das Problem analytisch auf eines reduziert werden, das nur einen Körper enthält. Viele Eigenschaften der endlich langen Reihe lassen sich an diesem Ersatzproblem studieren, z.B. Streuungswinkel, bestimmte Resonanzen usw.
Kanteneffekte, das heißt Eigenschaften, die das Verhalten am Anfang oder am Ende der endlich langen Reihe bestimmen, lassen sich mithilfe der unendlichen Reihe nicht studieren. Hier ist es möglich, das Problem durch eine Reihe periodisch angeordneter Körper zu approximieren, die sich nur in eine Richtung unendlich weit erstreckt, die sogenannte halb-unendliche Reihe. Dieses Problem ist analytisch schwieriger und numerisch wesentlich aufwendiger zu lösen als das der unendlichen Reihe. Allerdings lässt sich die Lösung der unendlichen Reihe verwenden, um numerisch effiziente Lösungsmethoden für die halb-unendliche Reihe zu konstruieren. Außerdem ermöglicht es die halb-unendliche Reihe, spezielle Resonanzen zu studieren, so genannte Rayleigh–Bloch-Wellen (auch surface waves oder guided waves), die entlang der Reihe propagieren, aber deren Amplitude mit größer werdendem Abstand von der Reihe exponentiell abfällt.