Adaptive mixed finite cell methods for elliptic problems
| Working Group: | WG Modelling and Scientific Computing |
| Leadership: |
Prof. Dr. Andreas Rademacher ((0421) 218 63831, E-Mail: arademac@uni-bremen.de)
Prof. Dr. Lothar Banz (E-Mail: lothar.banz@plus.ac.at) |
| Processor: | Dominika Thiede ((0421) 218-63833, E-Mail: dothiede@uni-bremen.de) |
| Funding: | Zentrale Forschungsförderung (ZF) der Universität Bremen |
| Project partner: | Paris Lodron Universität Salzburg |
| Time period: | 01.04.2022 - 31.03.2025 |
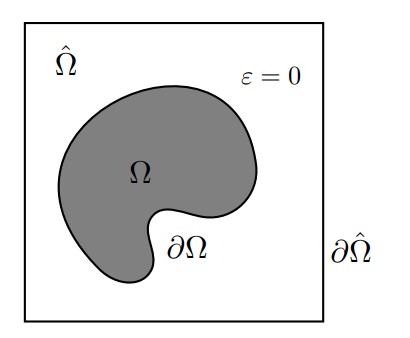 In many processes from metal-cutting manufacturing, e.g. grinding or milling, the workpiece changes its shape in a time-dependent manner and thereby exhibits very complex geometries. Since reproducing the workpiece as accurately as possible is essential in the simulation of such a process, various approaches have been developed in recent decades to efficiently address this challenge. One approach is the notional domain methods and the finite cell method (FCM) based on them. Their core idea is to embed the actual geometry into a simple domain (see illustration). The original geometry is described by an indicator function that is one in the actual domain and nearly zero outside. This approach has proven to be very efficient. However, it is a major and currently unsatisfactorily solved challenge to map the (frictional) contact of different bodies on the fictitious inner boundary. The present research project takes a first step towards tackling this problem. Here, a mixed FCM is developed and analyzed that can map fixed values of the solution on the fictitious boundary. This is an essential part of the task of solving contact problems. The focus is on ensuring the stability of the mixed approach using two different approaches, the question of convergence of the approaches, and the development of adaptive methods based on different error control techniques.
In many processes from metal-cutting manufacturing, e.g. grinding or milling, the workpiece changes its shape in a time-dependent manner and thereby exhibits very complex geometries. Since reproducing the workpiece as accurately as possible is essential in the simulation of such a process, various approaches have been developed in recent decades to efficiently address this challenge. One approach is the notional domain methods and the finite cell method (FCM) based on them. Their core idea is to embed the actual geometry into a simple domain (see illustration). The original geometry is described by an indicator function that is one in the actual domain and nearly zero outside. This approach has proven to be very efficient. However, it is a major and currently unsatisfactorily solved challenge to map the (frictional) contact of different bodies on the fictitious inner boundary. The present research project takes a first step towards tackling this problem. Here, a mixed FCM is developed and analyzed that can map fixed values of the solution on the fictitious boundary. This is an essential part of the task of solving contact problems. The focus is on ensuring the stability of the mixed approach using two different approaches, the question of convergence of the approaches, and the development of adaptive methods based on different error control techniques.

