Adaptive gemischte Finite Zellen Methoden für elliptische Probleme
| Arbeitsgruppe: | AG Modellierung und Wissenschaftliches Rechnen |
| Leitung: |
Prof. Dr. Andreas Rademacher ((0421) 218 63831, E-Mail: arademac@uni-bremen.de)
Prof. Dr. Lothar Banz (E-Mail: lothar.banz@plus.ac.at) |
| Bearbeitung: | Dominika Thiede ((0421) 218-63833, E-Mail: dothiede@uni-bremen.de) |
| Projektförderung: | Zentrale Forschungsförderung (ZF) der Universität Bremen |
| Projektpartner: | Paris Lodron Universität Salzburg |
| Laufzeit: | 01.04.2022 - 31.03.2025 |
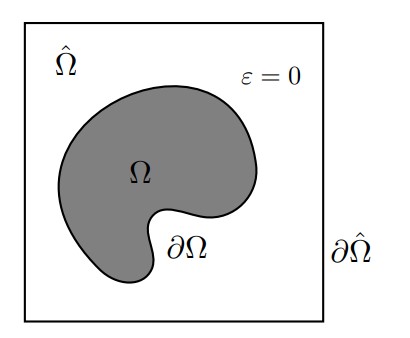 Bei vielen Prozessen aus der spanenden Fertigung, z.B. Schleifen oder Fräsen, ändert das Werkstück zeitabhängig seine Gestalt und weist dabei sehr komplexe Geometrien auf. Da die möglichst genaue Wiedergabe des Werkstücks in der Simulation eines solchen Prozesses wesentlich ist, sind in den letzten Jahrzehnten verschiedene Ansätze zur effizienten Bewältigung dieser Herausforderung entwickelt worden. Ein Ansatz ist die fiktive Gebiete Methoden und die darauf aufbauende Finite Zellen Methode (Finite Cell Method, FCM). Ihre Kernidee ist die Einbettung der eigentlichen Geometrie in ein simples Gebiet (siehe Illustration). Die originale Geometrie wird durch eine Indikatorfunktion, die Eins im eigentlichen Gebiet und nahezu Null außerhalb ist, beschrieben. Dieser Ansatz hat sich als sehr effizient erwiesen. Allerdings ist es eine große und aktuell noch unbefriedigend gelöste Herausforderung, den (reibungsbehafteten) Kontakt verschiedener Körper auf dem fiktiven inneren Rand abzubilden. Das vorliegende Forschungsvorhaben geht einen ersten Schritt zur Bewältigung dieser Aufgabenstellung. Hier wird eine gemischte FCM entwickelt und analysiert, die fest vorgegebene Werte der Lösung auf dem fiktiven Rand abbilden kann. Dabei handelt es sich um eine wesentliche Teilaufgabe bei der Lösung von Kontaktproblemen. Im Fokus stehen die Sicherstellung der Stabilität des gemischten Ansatzes mit Hilfe von zwei verschiedenen Ansätzen, die Frage nach der Konvergenz der Ansätze sowie die Entwicklung von adaptiven Methoden auf Basis verschiedener Fehlerkontrolltechniken.
Bei vielen Prozessen aus der spanenden Fertigung, z.B. Schleifen oder Fräsen, ändert das Werkstück zeitabhängig seine Gestalt und weist dabei sehr komplexe Geometrien auf. Da die möglichst genaue Wiedergabe des Werkstücks in der Simulation eines solchen Prozesses wesentlich ist, sind in den letzten Jahrzehnten verschiedene Ansätze zur effizienten Bewältigung dieser Herausforderung entwickelt worden. Ein Ansatz ist die fiktive Gebiete Methoden und die darauf aufbauende Finite Zellen Methode (Finite Cell Method, FCM). Ihre Kernidee ist die Einbettung der eigentlichen Geometrie in ein simples Gebiet (siehe Illustration). Die originale Geometrie wird durch eine Indikatorfunktion, die Eins im eigentlichen Gebiet und nahezu Null außerhalb ist, beschrieben. Dieser Ansatz hat sich als sehr effizient erwiesen. Allerdings ist es eine große und aktuell noch unbefriedigend gelöste Herausforderung, den (reibungsbehafteten) Kontakt verschiedener Körper auf dem fiktiven inneren Rand abzubilden. Das vorliegende Forschungsvorhaben geht einen ersten Schritt zur Bewältigung dieser Aufgabenstellung. Hier wird eine gemischte FCM entwickelt und analysiert, die fest vorgegebene Werte der Lösung auf dem fiktiven Rand abbilden kann. Dabei handelt es sich um eine wesentliche Teilaufgabe bei der Lösung von Kontaktproblemen. Im Fokus stehen die Sicherstellung der Stabilität des gemischten Ansatzes mit Hilfe von zwei verschiedenen Ansätzen, die Frage nach der Konvergenz der Ansätze sowie die Entwicklung von adaptiven Methoden auf Basis verschiedener Fehlerkontrolltechniken.

