TransWORHP
| Arbeitsgruppe: | AG Optimierung und Optimale Steuerung |
| Leitung: |
Prof. Dr. Christof Büskens ((0421) 218-63861, E-Mail: bueskens@math.uni-bremen.de )
Dr. Matthias Knauer ((0421) 218-63863, E-Mail: knauer@math.uni-bremen.de) |
| Bearbeitung: |
Dr. Matthias Knauer ((0421) 218-63863, E-Mail: knauer@math.uni-bremen.de)
Matthias Rick (E-Mail: mrick@uni-bremen.de) Hilke Behrends (E-Mail: hbehbend@math.uni-bremen.de) |
| Projektpartner: | |
| Laufzeit: | seit 01.01.2012 |
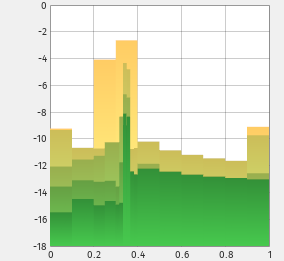
Viele Anwendungen aus dem Automobilbereich, der Luft- und Raumfahrt, der Robotik oder der Logistik führen auf Fragestellungen der Optimalen Steuerung. Hierbei soll ein dynamisches System unter Einhaltung von Nebenbedingungen von einem Anfangszustand in einen Endzustand überführt werden, so dass eine gegebene Zielfunktion minimiert wird.
Zur Lösung dieser Fragestellungen entwickelt die AG Optimierung und Optimale Steuerung das numerische Lösungsverfahren TransWORHP, das das unendlichdimensionale Optimalsteuerungsproblem in ein endlichdimensionales nichtlineares Optimierungsproblem umwandelt. Aufgesetzt auf das SQP-Verfahren WORHP lässt sich die Lösung unter Ausnutzung dünner Strukturen effizient berechnen.
Mit TransWORHP lassen sich zusätzlich Probleme lösen, die sich aus mehreren Phasen zusammensetzen. So können z.B. sämtliche Stufen eines Raketenstarts inklusive dem Absetzen von einem Satelliten gleichzeitig optimiert werden, oder alternative Flugbahnen simultan berechnet werden.
Zur Lösung der Dynamik auf einem diskreten Zeitgitter können unterschiedliche Integrationsverfahren gewählt werden. Um die Genauigkeit der Lösung zu erhöhen, lässt sich dieses Zeitgitter adaptiv verfeinern. Alternativ stehen Multiple-Shooting-Techniken zur Verfügung, die auf kleinere Problemgrößen führen, und sich besser für Probleme mit großem Zeithorizont eignen, etwa für die Trajektorienberechnung bei Weltraum-Missionen.
Ergebnisse der parametrischen Sensitivitätsanalyse mit dem Modul WORHP Zen stehen zusätzlich in TransWORHP zur Verfügung und können z.B. zur Optimalsteuerung unter Echtzeitanforderungen benutzt werden.
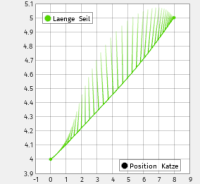 Lösung der Bewegung eines Kransystems mit Sensitivitätsdifferentialen bzgl. Fehlern in der Start-auslenkung.
Lösung der Bewegung eines Kransystems mit Sensitivitätsdifferentialen bzgl. Fehlern in der Start-auslenkung.
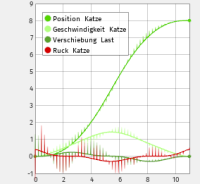 Lösung der Bewegung eines Kransystems mit Sensitivitätsdifferentialen bzgl. Fehlern in der Start-auslenkung.
Lösung der Bewegung eines Kransystems mit Sensitivitätsdifferentialen bzgl. Fehlern in der Start-auslenkung.
Umbei Ansprechpartnern aus der Industrie den technischen Stand dieses Ansatzes präsentieren zu können, entstand zudem eine grafische Oberfläche, die es erlaubt, beliebige Probleme einzugeben und die Ergebnisse visualisieren zu können. Optimalsteuerungsprobleme können hier mit dem Ansatz der sogenannten modellprädiktiven Regelung ebenfalls iterativ und extrem effizient gelöst werden.
Publikationen
- M. Knauer, C. Büskens.
Real-Time Optimal Control Using TransWORHP and WORHP Zen.
Modeling and Optimization in Space Engineering, G. Fasano, J. D. Pintér (Hrsg.), Springer Optimization and Its Applications, vol 144, S. 211-232, Springer Verlag, 2019.