Regularisierungsverfahren in Banachräumen angewandt auf inverse Streuprobleme
| Arbeitsgruppe: | Ehemalige AG Inverse Probleme |
| Leitung: | Prof. Dr. Armin Lechleiter |
| Bearbeitung: |
Dr.-Ing. Florian Bürgel
Dr. Marcel Rennoch |
| Projektförderung: | DFG - Deutsche Forschungsgemeinschaft |
| Projektpartner: | |
| Laufzeit: | 16.07.2014 - 16.10.2017 |
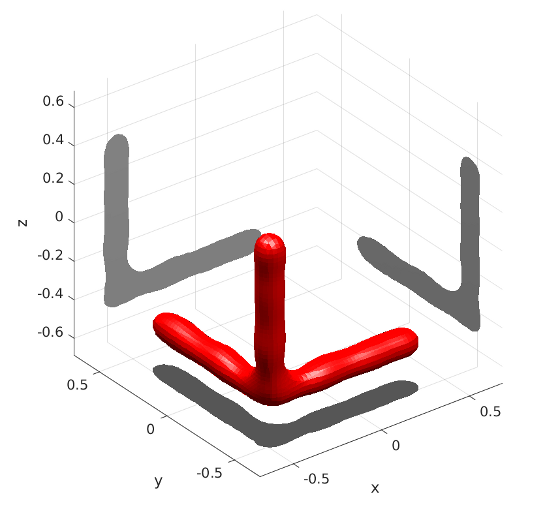
Die Betrachtung von inversen Streuproblemen in bestimmten Anwendungsbereichen, wie z.B. der Materialprüfung, erlaubt die Annahme, dass der Kontrast des zu rekonstruierenden Objekts einen aus nur wenigen Nicht-Null-Einträgen bestehenden Träger, sprich eine sparse Natur, hat. Berücksichtigt man bei der Rekonstruktion dieses sparsity-Konzept, so führt das auf Regularisierungsverfahren, deren Strafterme nicht mehr in Hilbert-, sondern in Banachräumen liegen.
Auch wenn dieses Konzept in der Bild- und Signalverarbeitung im letzten Jahrzehnt zu einer Vielzahl an Forschungsergebnissen geführt hat, ist es im Bereich der Streutheorie eher unbeachtet geblieben. In diesem Projekt versuchen wir daher sparsity-Regularisierungsverfahren für inverse Streuprobleme und daraus folgend schnelle und effiziente Algorithmen zu entwickeln. Langfristig sollen die Ergebnisse auch in bestehende Kooperationen mit Partnern anderer Fachbereiche eingebracht werden.
Publikationen
- F. Bürgel, K. Kazimierski, A. Lechleiter.
IPscatt—A MATLAB Toolbox for the Inverse Medium Problem in Scattering.
ACM Transactions on Mathematical Software, 45(4), 45:1–45:20, 2019.DOI: 10.1145/3328525
- F. Bürgel, K. Kazimierski, A. Lechleiter.
A sparsity regularization and total variation based computational framework for the inverse medium problem in scattering.
Journal of Computational Physics, 339, 1–30, 2017. - A. Lechleiter, M. Rennoch.
Non-linear Tikhonov Regularization in Banach Spaces for Inverse Scattering from Anisotropic Penetrable Media.
Inverse Problems and Imaging, 11(1):151-176, 2017.DOI: 10.3934/ipi.2017008
- M. Rennoch.
Regularization Methods in Banach Spaces Applied to Inverse Medium Scattering Problems.
Dissertationsschrift, Universität Bremen, 2017.online unter: Elektronische Bibliothek der Universität Bremen

