Parallele Algorithmen zur Modellreduktion von hochdimensionalen linearen Regelungssystemen
| Arbeitsgruppe: | Ehemalige AG Numerik |
| Leitung: |
Prof. Dr. Angelika Bunse-Gerstner (E-Mail: bunse-gerstner@math.uni-bremen.de )
Prof. Dr. Peter Benner |
| Bearbeitung: | |
| Projektförderung: | DAAD (Acciones Integradas Hispano-Alemanas) |
| Projektpartner: |
Prof. Dr. H. Faßbender, TU München Prof. Dr. E. Quintana-Ortí, Universitat Jaume I, Castellón, Spanien |
| Laufzeit: | 01.01.1998 - 30.06.2002 |
 In diesem Projekt wurden parallelisierbare Algorithmen zur Modellreduktion linearer geregelter Systeme der Form
In diesem Projekt wurden parallelisierbare Algorithmen zur Modellreduktion linearer geregelter Systeme der Form
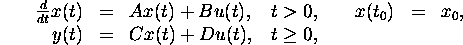
Oft enthalten physikalische Modelle Redundanzen, insbesondere wenn sie durch automatische Modellierungstools wie Dymola oder Modelica generiert werden. Darüber hinaus ist die Zustandsraumdimension n aufgrund des gewählten Modellierungsansatzes häufig zu groß, um das Systemverhalten zu simulieren oder in der Praxis zu realisieren. Insbesondere ist das der Fall, wenn das System aus der Semidiskretisierung einer partiellen Differentialgleichung, z.B. durch eine Finite-Elemente-Methode, hervorgegangen ist. In diesem Fall ist die Koeffizientenmatrix A üblicherweise sparse, d.h. dünnbesetzt und n ist sehr groß (n > 10.000). Aber auch die Modellierung mit gewöhnlichen Differentialgleichungen kann auf sehr große, evtl. dichtbesetzte Koeffizientenmatrizen führen, z.B. bei der Modellierung chemischer Prozesse oder flexibler Strukturen der Raumfahrt bzw. mechanischer Mehrkörpersysteme, bei der Analyse und dem Entwurf von Schaltkreisen (VLSI Design) und anderen Bereichen der Mikrosystemtechnik. Die Dimension des Zustandsraums bei solchen Problemen liegt oft bei einigen Hundert bis zu 10.000.
Da der Reglerentwurf üblicherweise ein iterativer Prozess ist, der in einer Computer-Aided Control System Design (CACSD) Entwicklungsumgebung wie z.B. Scilab oder Simulink/Matlab® stattfindet und eine Vielzahl von Berechnungen mit den Systemdaten erfordert, die mindestens kubisch von der Zustandsraumdimension und der Anzahl der Ein- und Ausgänge abhängen, möchte man das System durch ein System niedrigerer Ordnung approximieren, das die Eigenschaften und das dynamische Verhalten des Originalsystems möglichst gut wiedergibt. Man versucht also, ein Regelungssystem zu finden, das zu gegebenem Eingangssignal möglichst genau das Ausgangssignal des Originalsystems approximiert und darüber hinaus keine Redundanzen mehr enthält.
In diesem Projekt wurden für Systeme mit dichtbesetzten Koeffizientenmatrizen neue parallele Modellreduktionsalgorithmen entwickelt und, basierend auf ScaLAPACK und parallelen BLAS, für Parallelrechner mit verteiltem Speicher implementiert. Die Kommunikation der implementierten Routinen setzt auf dem MPI Standard auf und verwendet die Basic Linear Algebra Communication Subprograms (BLACS). Basierend auf den im Vorgängerprojekt Parallele Algorithmen für linear-quadratische Optimalsteuerungsprobleme entwickelten und in der Parallel Library in Control (PLiC) implementierten Methoden zur Berechnung von Faktoren der semidefiniten Lösungen von linearen Matrixgleichungen wurden effiziente neue Algorithmen entwickelt, die auf der Idee des balancierten Abschneidens mithilfe der Gramschen Matrizen des Systems basieren. Diese sind besonders effizient für große Systeme, bei denen oft die Hankel-Singulärwerte schnell abfallen, da statt der Singulärwertzerlegung (SVD) einer n x n Matrix (bei herkömmlichen Verfahren) nur noch die SVD einer viel kleineren Matrix berechnet werden muss. Die neu entwickelten Verfahren eignen sich insbesondere für Parallelrechner mit verteiltem Speicher, da die benötigte lineare Algebra auf solchen Architekturen wesentlich effizienter ist als bei Schurvektor-basierten Methoden, wie sie z.B. in den Modellreduktionsroutinen in SLICOT (Subroutine Library in Control Theory) verwendet werden. In ähnlicher Weise wurde ein Verfahren basierend auf dem balancierten stochastischen Abschneiden realisiert, indem die in der PLiC verfügbaren Verfahren zur Lösung von algebraischen Riccati-Gleichungen verwendet wurden. Alle implementierten Routinen wurden in einer Unterbibliothek der PLiC integriert. Diese ist als PLiCMR unter http://spine.act.uji.es/~plicmr verfügbar. Um eine einfache Möglichkeit der Bedienung zu schaffen, wurde ein Java-basiertes Web-Interface erstellt, das Anwendern die Möglichkeit bietet, ihr zu reduzierendes Modell auf einen Linux-PC Cluster in Castellón hochzuladen und "remote" auf dem Parallelrechner die Systemreduktion mit dem gewünschten Algorithmus durchzuführen. Das reduzierte Modell wird dem Anwender dann per Email zugesendet.

