Fehlerabschätzungen und Adaptive Finite-Elemente-Methoden für monotone semi-lineare Probleme
| Arbeitsgruppe: | AG Numerik PDE |
| Leitung: | Prof. Dr. Alfred Schmidt ((0421) 218-63851, E-Mail: alfred.schmidt@uni-bremen.de ) |
| Bearbeitung: | |
| Projektpartner: |
Prof. Dr. Kunibert G. Siebert, Universität Duisburg-Essen Prof. Dr. Ricardo H. Nochetto, University of Maryland, College Park, USA Dr. Andreas Veeser, Universität Mailand, Italien |
| Laufzeit: | seit 01.04.2002 |
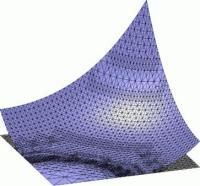
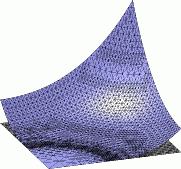 Gleichungen mit monotonen, semi-linearen Operatoren treten in vielen physikalischen Anwendungen auf, zum Beispiel in der Theorie pseudoplastischer Fluide oder bei relativistischen Modellen für schwarze Löcher. In Zusammenarbeit mit den Projektpartnern wurden für solche Probleme Abschätzungen für die punktweisen Fehler einer Finite-Elemente-Approximation hergeleitet sowie deren Effizienz bewiesen. Im Unterschied zu den üblichen Techniken für Integral-Normen des Fehlers basieren die Beweise hier auf der Konstruktion von geeigneten Barrieren-Funktionen. Darauf aufbauende, adaptive Methoden erlauben die automatische Steuerung einer lokalen Gitterverfeinerung, so dass der punktweise Fehler unter einer vorgegebenen Toleranz bleibt.
Gleichungen mit monotonen, semi-linearen Operatoren treten in vielen physikalischen Anwendungen auf, zum Beispiel in der Theorie pseudoplastischer Fluide oder bei relativistischen Modellen für schwarze Löcher. In Zusammenarbeit mit den Projektpartnern wurden für solche Probleme Abschätzungen für die punktweisen Fehler einer Finite-Elemente-Approximation hergeleitet sowie deren Effizienz bewiesen. Im Unterschied zu den üblichen Techniken für Integral-Normen des Fehlers basieren die Beweise hier auf der Konstruktion von geeigneten Barrieren-Funktionen. Darauf aufbauende, adaptive Methoden erlauben die automatische Steuerung einer lokalen Gitterverfeinerung, so dass der punktweise Fehler unter einer vorgegebenen Toleranz bleibt.