Vorkonditionierung für schnelle Löser zur Berechnung elektromagnetischer Felder
| Arbeitsgruppe: | Ehemalige AG Numerik |
| Leitung: | Prof. Dr. Angelika Bunse-Gerstner (E-Mail: bunse-gerstner@math.uni-bremen.de ) |
| Bearbeitung: | Dr. Ignacio Gutiérrez-Cañas |
| Projektpartner: | EADS Deutschland GmbH, Betriebsstätte Bremen |
| Laufzeit: | 01.06.2000 - 28.02.2006 |

Die AG Numerik und der Kooperationspartner EADS (European Aeronautic Defence and Space Company) in Bremen führen seit mehreren Jahren eine Kooperation durch, die sich mit der schnellen Berechnung des elektromagnetischen Feldes in Gegenwart großer, elektrischer Streukörper, wie z.B. Flugzeuge oder Satelliten, und Sendeanlagen beschäftigt. Die mathematische Formulierung dieser Probleme erfolgt u.a. durch die Electric Field Integral Equation (EFIE), deren Diskretisierung zu linearen Gleichungssystemen mit sehr großen, dichtbesetzten Koeffizientenmatrizen führt. Dies hat zur Folge, dass für praxisrelevante Probleme, bei denen die Anzahl der Unbekannten zwischen 104 und 107 liegt, die Matrix nicht mehr vollständig aufgestellt, sondern nur der Nahfeldanteil explizit gespeichert werden kann. Zur Lösung des linearen Gleichungssystems müssen iterative Verfahren verwendet werden, die in jedem Iterationsschritt nur ein Matrix-Vektor-Produkt benötigen. Dieses wird für den Fernfeldanteil mithilfe der Fast-Multipole-Methode realisiert, die durch einen Multilevel- Ansatz beschleunigt wird.
In einer früheren Phase des Projekts wurden verschiedene iterative Gleichungssystemlöser in das vorhandene Software-Paket integriert und getestet. Allein mit der guten Wahl eines iterativen Lösers sind die bei der Berechnung auftretenden Probleme jedoch nicht zu beheben. Nur mit einem geeigneten Vorkonditionierer ist eine Konvergenz der Verfahren bei großen Dimensionen überhaupt erreichbar. Die Entwicklung von effektiven Vorkonditionierern für die auftretenden Gleichungssysteme ist daher für den Lösungsprozess von entscheidender Bedeutung. Es wurde eine auf die vorliegende Matrixstruktur angepasste Version der Vorkonditionierung mit einer Sparsen Approximativen Inversen (SPAI) entwickelt und implementiert. Hiermit konnte im Vergleich mit anderen gängigen Vorkonditionierungen eine zunächst befriedigende Beschleunigung des Lösungsprozesses erzielt werden. Eine weitere Vorkonditionierung, die gute Ergebnisse gezeigt hat, besteht in der Anwendung von Inner-Outer-Methoden beim Lösen mit GMRES. Dabei wurde das innere Gleichungssystem ausschließlich mit der Nahfeldmatrix gelöst.
Allerdings verringert sich bei wachsender Dimension des Gleichungssystems die beschleunigende Wirkung dieser Vorkonditionierer, da der Nahfeldanteil, auf dem beispielsweise SPAI grundlegend basiert, gleichermaßen abnimmt. Folglich sind weitere Verbesserungen unter anderen Gesichtspunkten erforderlich. Ein möglicher Aspekt ist die Betrachtung der speziellen Rangstruktur der Fernfeldmatrix, die auch die Fast-Multipole- Methode ausnutzt.
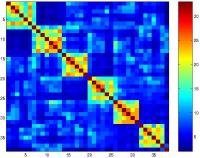
In der Regel haben die oben genannten, resultierenden Matrizen vollen Rang. Betrachtet man aber den effektiven Rang ihrer Blöcke, so kommt eine sehr interessante Rangverteilung zum Vorschein. Die Abbildung zeigt die Rangverteilung für ein sehr stark vereinfachtes Satellitenmodell. Offensichtlich haben die Matrixblöcke, die weit von einem gewissen Band um die Diagonale entfernt liegen, nur einen kleinen effektiven Rang. Matrizen mit dieser Eigenschaft fallen in die Kategorie der so genannten semiseparablen Matrizen. Die Verwendung einer Approximation an die Koeffizientenmatrix unter Ausnutzung dieser Rangstruktur ist ein weiterer gewinnbringender Entwicklungsschritt bei der Inner-Outer- Methode.
Aufgrund der durchgeführten Experimente ist zu erkennen, dass diese Verbesserung der Vorkonditionierung nicht nur eine vielversprechende Bereicherung ist, sondern auch eine neue Perspektive für die Betrachtung dieser Problemklasse eröffnet.