Beweis durch zentrische Streckung

Beide Beweise zeigen, dass die Seitenhalbierende s_a von s_b so geschnitten wird, dass der Schnittpunkt S s_a im Verhältnis 2:1 teilt. Analog schneidet auch s_c die Seitenhalbierende s_a so, dass dieser Schnittpunkt s_a im Verhältnis 2:1 teilt. Also muss der Schnittpunkt von s_a mit s_b der gleiche sein wie der Schnittpunkt von s_a mit s_c. Folglich verlaufen alle drei Seitenhalbierende durch einen Punkt.

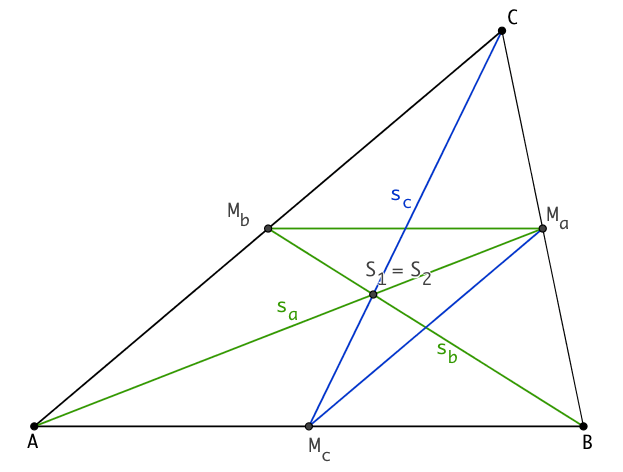
Die Mittellinie M_aM_b ist parallel zu AB und halb so lang. Der Schnittpunkt von s_a mit s_b sei S₁.
Dann bildet die zentrische Streckung an S₁ mit dem Streckfaktor -2 die Strecke M_aM_b auf die Strecke AB ab (grüne Linien). Dann gilt auch 2*| S₁M_a | = | S₁A | .
Nun sei S₂ der Schnittpunkt von s_a mit s_c. Analog zeigt man, dass die Strecke M_aM_c durch eine zentrische Streckung an S₂ mit dem Streckfaktor -2 auf die Strecke AC abgebildet wird (blaue Linien). Dann gilt auch 2*| S₂M_a | = | S₂A | .
Damit gilt aber, dass der Schnittpunkt S₁ von s_a mit s_b mit dem Schnittpunkt S₂ von s_a mit s_c übereinstimmt. Also schneiden sich alle drei Seitenhalbierenden in einem Punkt.

R. Albers, Erstellt mit GeoGebra