Beweis durch Strahlensätze

Beide Beweise zeigen, dass die Seitenhalbierende s_a von s_b so geschnitten wird, dass der Schnittpunkt S s_a im Verhältnis 2:1 teilt. Analog schneidet auch s_c die Seitenhalbierende s_a so, dass dieser Schnittpunkt s_a im Verhältnis 2:1 teilt. Also muss der Schnittpunkt von s_a mit s_b der gleiche sein wie der Schnittpunkt von s_a mit s_c. Folglich verlaufen alle drei Seitenhalbierende durch einen Punkt.

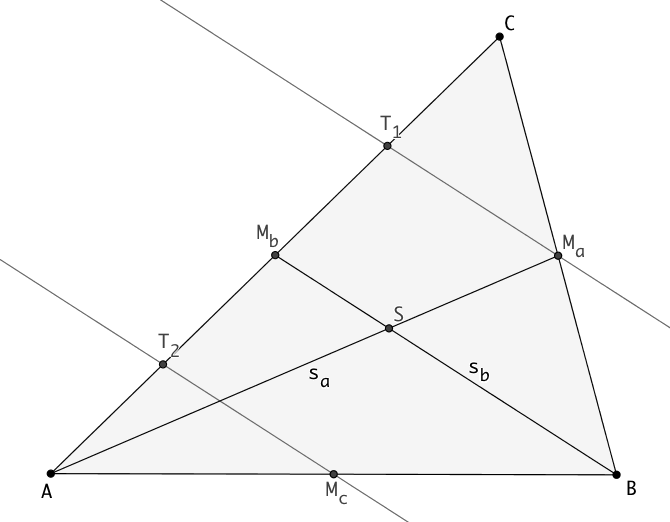
Zusätzlich zu den beiden Seitenhalbierenden s_a und s_b zeichnet man die Parallelen zu s _b durch M_a und M_c (graue Linien). Diese Parallelen schneiden die Strecke AC in den Punkten T₁ und T₂.
Nach dem 1. Strahlensatz mit dem Zentrum A ist T₂ die Mitte der Strecke AM_b, da M_c die Mitte der Strecke AB ist.
Nach dem 1. Strahlensatz mit dem Zentrum C ist T₁ die Mitte der Strecke CM_b, da M_a die Mitte der Strecke CB ist.
Damit teilen die Punkte T₂, M_b und T₁ die Strecke AC in Viertel. Also ist die Strecke AM_b ²/₃ der Strecke AT₁. Dieses Streckenverhältnis wird mit dem 1. Strahlensatz mit dem Zentrum A übertragen auf die Strecke AM_a. Somit ist die Strecke AS ²/₃ der Strecke AM_a.

R. Albers, Erstellt mit GeoGebra