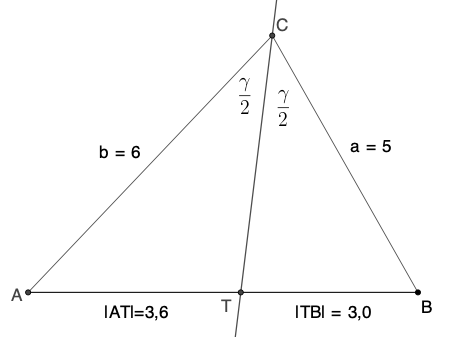
Es sei T ein innerer Punkt der Dreiecksseite AB. Dann ist T der Schnittpunkt der Winkelhalbierenden des Winkels ∡ACB genau dann, wenn gilt $\frac{|AT|}{|TB|}=\frac{|AC|}{|CB|}$.

Beweis
"T Schnitt der Winkelhalbierenden $⇒\frac{|AT|}{|TB|}=\frac{|AC|}{|CB|}$"
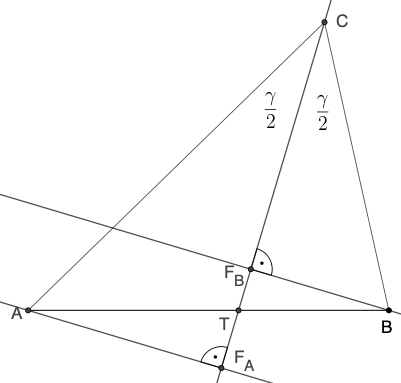
Vom Punkt A wird das Lot auf die Winkelhalbierende gefällt, Fußpunkt F_A.  Ebenso wird von B das Lot auf die Winkelhalbierende gefällt, Fußpunkt F_B. Dann sind die Dreiecke △AF_AT und △TBF_B ähnlich (rechte Winkel, Scheitelwinkel bei T). Also gilt $\frac{|AT|}{|TB|}=\frac{|AF_A|}{|BF_B|}$.

Weiterhin sind die Dreiecke △AF_AC und △CF_BB ähnlich (rechter Winkel, $\frac{γ}{2}$ bei C). Also gilt $\frac{|AF_A|}{|BF_B|}=\frac{|AC|}{|CB|}$.
Setzt man beide Gleichungen zusammen, erhält man die behauptete Gleichung  $\frac{|AT|}{|TB|}=\frac{|AC|}{|CB|}$

" $\frac{|AT|}{|TB|}=\frac{|AC|}{|CB|}⇒$<T Schnitt der Winkelhalbierenden"
Die Verhältnisgleichung legt für T das Teilungsverhältnis fest. Das gleiche Teilungsverhältnis gilt für den Schnittpunkt der Winkelhalbierenden mit AB. Wegen der Eindeutigkeit eines inneren Teilungspunktes bei gegebenen Teilungsverhältnis muss die Gerade TC die Winkelhalbierende des Winkels γ  sein.

R. Albers, erstellt mit GeoGebra